‍What is the Controlled NOT Gate?

Qubits have their classical counterpart: the bit. Similarly, the classical logic gate has its own quantum analog. Matrices are used to describe these logical quantum gates which one can impose upon a qubit. An example is the Pauli X-gate, which approximates the classical NOT operation.

In order to fully realize any possible logical operation, one must use a list of gates which creates a universal gate set. At least one multi-qubit gate is required to encompass the property of entanglement. A popular choice is the Controlled NOT (CNOT) gate, which emulates the classical XOR gate. The popularity of this choice stems from the universal gate set formed by the single-qubit rotation gates (Pauli X , Y, Z, I), or any other single arbitrary rotation gate set, combined with an entangling gate like the CNOT. Single qubit Pauli gates are extremely useful for qubit rotation, typically visualized across the Bloch sphere. Hence, the CNOT is a popular choice for gate selection when realizing quantum gates on physical hardware. 

What does the CNOT Gate Do?

The CNOT gate is a two qubit operation. Its quantum circuit visualization is provided above. One qubit serves as the control qubit (black dot), while the other serves as the data qubit (empty circle with a cross). The gate input/output is: 

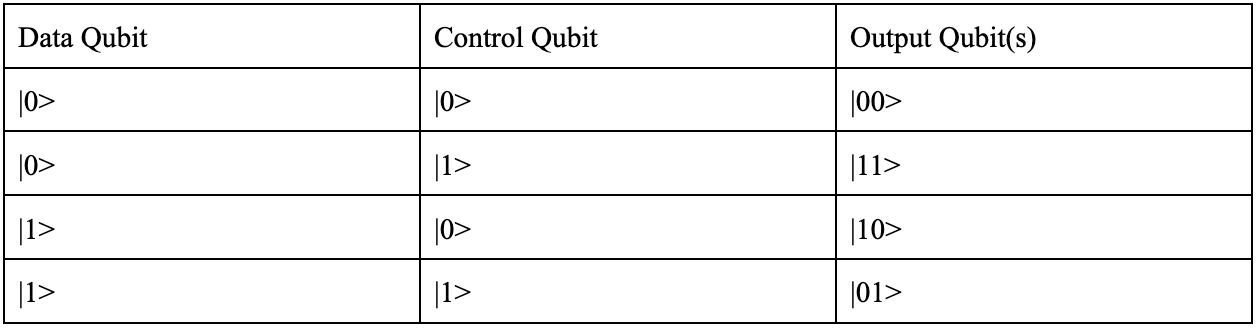
The data qubit has a state which is dependent on the control qubit. The operation of the CNOT gate is as follows: if the control qubit is in the |1> state, then the data qubit will have its state flipped. The control qubit state will always stay the same.

Importance of the CNOT in Algorithms

There are many quantum algorithms which rely upon the CNOT gate for their typical circuit representations. Examples of these include the Quantum Fourier Transform (QFT) and related algorithms, variational quantum algorithms, or the setup for Grover's Algorithm. In fact, the majority of quantum algorithms require the use of the CNOT gate, or entangling alternatives, to realize entanglement in quantum hardware. Thus, the gate fidelity of the CNOT gate is of extreme importance to quantum systems, especially considering two-qubit implementation often proves more difficult than single-qubit gate implementation. As a result, a common standard is to measure quantum circuits based upon the total number of CNOT gates in an algorithm, especially among Hamiltonian designs in variational quantum algorithms. For a deeper explanation, see circuit depth.

Realizations of CNOT in Physical Hardware

The realization of the CNOT, and other multi-qubit gates, is modality and system dependent. This section will briefly focus on the mechanism employed by QuEra for multi-qubit gates: the Rydberg Blockade. 

Rydberg States are highly energized atomic states. If we are able to place a neutral atom in a Rydberg State, it will experience strengthened atomic properties, such as the van der Waals and dipole-dipole interatomic forces. These strengthened forces can prevent nearby states from entering the same energetic state, allowing for use of conditional logic. Natively, this represents the controlled-Z (CZ) gate, but this logic can be combined with Pauli rotations to form the CNOT (or CX) gate. For a deeper explanation including advantages and disadvantages of this mechanism, see Rydberg Blockade.